Het gebeurt regelmatig dat mensen tijdens een A/B-test de bezoekersverdeling aanpassen, bijvoorbeeld als de ene variant beter scoort dan de andere. Dit kan er echter voor zorgen dat een verkeerde conclusie wordt getrokken. Je riskeert namelijk een zogenaamde Simpsons paradox.
Tekst: Annemarie Klaassen
De statistische situatie waarin een trend of relatie wordt geobserveerd tussen verschillende groepen, die weer verdwijnt op het moment dat de groepen worden gecombineerd, heet Simpsons paradox. Dit principe wordt vaak over het hoofd gezien.
Werking
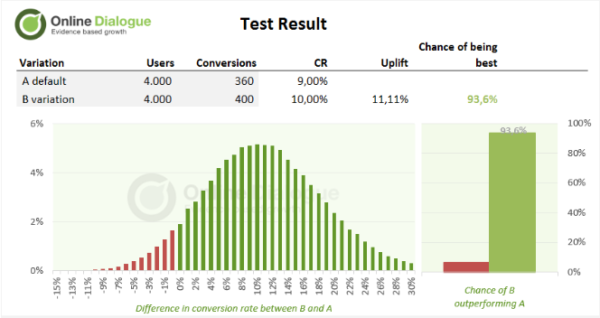
Stel dat je een A/B-test start vlak voor het weekend en je verdeelt het verkeer netjes fiftyfifty - elke variant krijgt tweeduizend bezoekers per dag. Na het weekend bekijk je de eerste resultaten en zie je dat B al twee dagen een stuk beter presteert dan A (zie afbeelding 1).
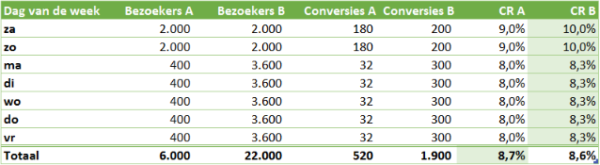
Het conversiepercentage van variant B ligt 11,11 procent hoger dan dat van A. Een Bayesiaanse calculatie laat zelfs zien dat de kans dat B beter is dan A, 93,6 procent is. Hierop besluit je de bezoekersverdeling van de test aan te passen naar 10/90: vanaf maandag krijgt 10 procent van het bezoek variant A te zien en 90 procent de beter presterende variant B. Je houdt de statistieken nauwlettend in de gaten en ziet tot je tevredenheid dat B het beter blijft doen dan A (alhoewel het verschil minder groot wordt). Wanneer de test een volle week heeft gedraaid eindigt de test en maak je de balans op. En wat blijkt: op totaalniveau presteert variant A beter dan variant B! Variant A heeft een uiteindelijk conversiepercentage van 8,7 en variant B van 8,6 (zie afbeelding 2).
Hier zie je Simpsons paradox vol in werking: op elke afzonderlijke dag presteert variant B beter dan A, maar als je de groepen combineert is er een ander beeld te zien. Dit wordt veroorzaakt doordat de groepen ongelijk verdeeld zijn én er een derde variabele invloed heeft op de conversie, namelijk de dag van de week. Doordeweeks liggen de conversiepercentages lager dan in het weekend en de verschillen tussen A en B zijn dan ook minder groot.
Wees altijd kritisch
Je mag dus tijdens de duur van de A/B-test de bezoekersverdeling nooit aanpassen. Er kunnen namelijk altijd derde variabelen aan het werk zijn. Zorg daarom dat je altijd kritisch bent bij het trekken van conclusies. Segmenteer de geaggregeerde data op betekenisvolle dimensies (indien random verdeeld) en bepaal of de conclusie hout snijdt. Vind je per segment toch een tegenovergesteld effect? Herhaal de test dan in een nieuwe speciaal getargete A/B-test om de bevindingen te valideren.
__________
Dit artikel is geschreven door Annemarie Klaassen, analytics & optimization expert bij Online Dialogue, voor het online analyse en optimalisatieplatform Webanalisten.nl. Het volledige artikel vind je hier.
__________
Dit artikel verscheen eerder in Twinkle 2-2017.

Er is op dit moment 0 keer gereageerd op:
Pas op voor Simpsons paradox
Je kunt niet meer reageren op dit artikel.